Prosta regresja jednoczynnikowa jest podobna do wzoru matematycznego, który poznaliśmy już w szkole podstawowej. Jest to wzór pozbawiony czynnika losowego.
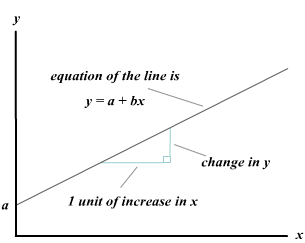
Zgodnie z zasadami algebry równanie linii prostej w układzie osi X, Y opisuje się wzorem:
Model ten ma prostą postać, którą można przedstawić graficznie:
Aby zrozumieć jak działa taki model wystarczy za x1 wstawić jakąś wartość wtedy w wyniku obliczeń uzyskamy y1. Uzyskamy punkt o współrzędnych (x1,y1). Dalej podstawiając inne wartości x2, x3, x4 uzyskamy y1, y2, y3 łącząc te punkty uzyskamy linię prostą o równaniu Y= A+BX.
Najprostszy model regresji liniowej populacji ma postać:
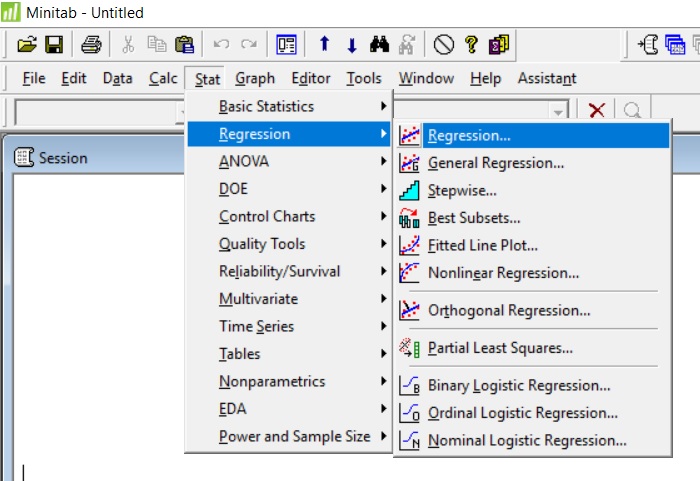
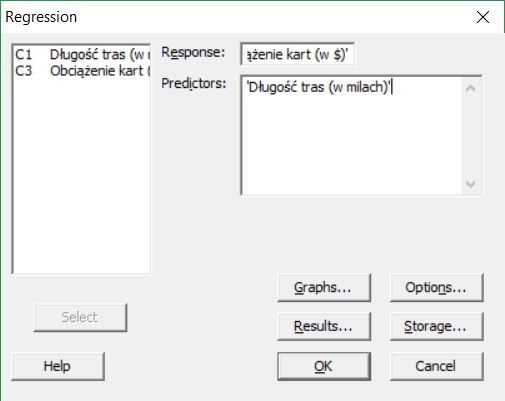
Przykład tworzenia prostego modelu regresji w programie Minitab
Dane pochodzą z książki Amir Aczel str. 469, dane można z ciągnąć tutaj.
| Długość tras (w milach) | Obciążenie kart (w $) |
| 1211 | 1802 |
| 1345 | 2405 |
| 1422 | 2005 |
| 1687 | 2511 |
| 1849 | 2332 |
| 2026 | 2305 |
| 2133 | 3016 |
| 2253 | 3385 |
| 2400 | 3090 |
| 2468 | 3694 |
| 2699 | 3371 |
| 2806 | 3998 |
| 3082 | 3555 |
| 3209 | 4692 |
| 3466 | 4244 |
| 3643 | 5298 |
| 3852 | 4801 |
| 4033 | 5147 |
| 4267 | 5747 |
| 4498 | 6420 |
| 4533 | 6059 |
| 4804 | 6426 |
| 5090 | 6321 |
| 5233 | 7026 |
| 5439 | 6964 |
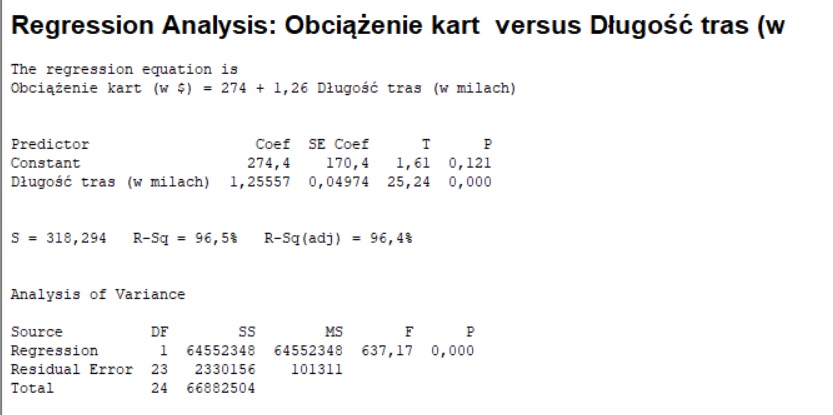
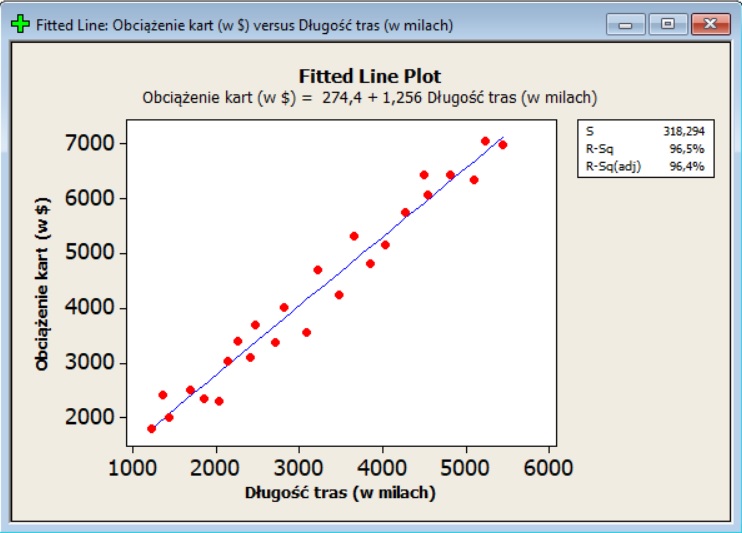
Wykonaliśmy model regresji dla danych empirycznych załączonych do tego wpisu.
Prosta regresja jednoczynnikowa jest wyrażona wzorem 23.1, która dla tych danych przybiera postać:
Równanie linia regresji ma następującą postać:
W kolejnych wpisach nauczymy się interpretować oraz oceniać moc regresji. Nauczymy się również szacować standardowe błędy estymatorów parametrów regresji.
Prosta regresja jednoczynnikowa jako równanie dopasowania prostej do danych w układzie X, Y. Równanie takie możemy również uzyskać w Minitab w inny sposób.