Ideą analizy porównawczej two-sample t jest porównanie średnich dwóch zbiorów. Sprawdzane jest, czy średnie dla dwóch zbiorów pomiarów są sobie równe.
Takie zadanie może wydawać się lekko infantylne. Przecież wystarczy policzyć średnie obu zbiorów i porównać je do siebie.
Należy zdać sobie sprawę, że dwa zestawy danych są próbami dwóch populacji. Ich średnie są, więc tylko estymacjami prawdziwych średnich z populacji. Ważnym elementem jest moc testu, czyli prawdopodobieństwo prawidłowego odrzucenia hipotezy zerowej mówiącej o tym, że średnie obu populacji są sobie równe. Moc testu jest tożsama z współczynnikiem ufności, przyjmowanym zwykle na poziomie 95
Badania statystyczne specjalizują się w szacowaniu parametrów populacji na podstawie niewielkich wycinków tych populacji
W tym wpisie przedstawiony zostanie przykład zastosowania analizy porównawczej two-sample t przy małych zbiorach obserwacji.
Porównanie dwóch protokołów zachowań obsługi klienta
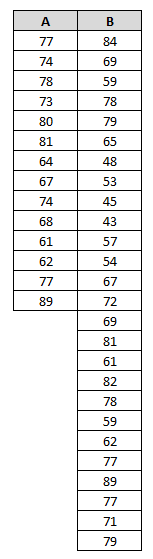Duży ogólnopolski bank specjalizujący się w obsłudze klientów wprowadził dwa eksperymentalne protokoły zachowań obsługi klienta. W dwóch losowo wybranych bankach zaczęto stosować oddzielnie oba eksperymentalne protokoły obsługi. Dokonano pomiaru zadowolenia klientów z obsługi w punktach detalicznych. Niestety budżet nie pozwolił na zbadanie dużej liczby klientów. Zbadano, więc opinie niespełna kilkudziesięciu osób.
Proszę o zbadanie czy protokoły A i B istotnie różnią się w kontekście wpływu na zadowolenie klientów banku.
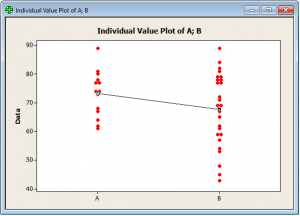
Porównanie graficzne
Pierwszym krokiem analizy porównawczej obu zestawów pomiarów jest porównanie graficzne.
Wykres punktowy wskazał, że klienci banku bardziej docenili procedurę A. Należy zauważyć, że liczba pomiarów procedury A jest istotnie mniejsza od pomiarów procedury B. Linia prosta wskazuje na średnią obu próbek. Punkty rozłożone są równo, co wskazuje na rozkład noramlny obu zestawów.
Normalność zbioru pomiarów jest warunkiem koniecznym stosowania analizy porównawczej two-sample t .
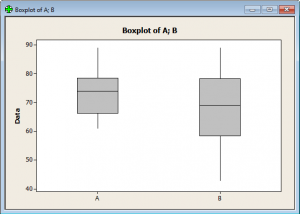
Bardzo przydatnym wykresem do porównywania zbiorów jest boxplot. Linie przecinające pudełka oznaczają mediany, wąsy symbolizują zmienność wyników. Wykres pudełkowy potwierdził, że klienci są bardziej zadowoleni z obsługi w procedurze A (mediana 74
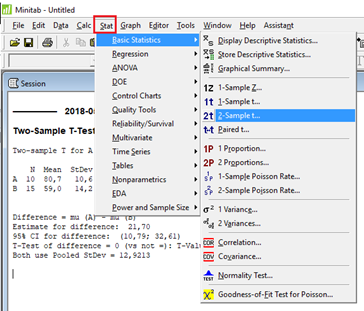
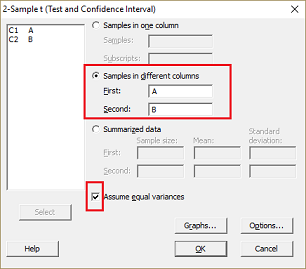
Test równości dwóch średnich populacji
Test analizy porównawczej two-sample t studenta daje dwie statystyki, informujące o różnicy bądź braku różnic między średnimi: statystykę t i p-value. Wartość t służy do określenia wartości p-value. Wartość p-value wskazuje, jakie jest prawdopodobieństwo, że zachowanie hipotezy o równości średnich H0: µA = µB jest prawdziwe. Standardowo współczynnik ufności przyjmuje się na poziomie 95
Wartość p-value jest większa od 0,05, co oznacza, że nie ma podstaw do odrzucenia hipotezy zerowej mówiącej o istotnej różnicy pomiędzy średnim zadowoleniem klientów w protokołach A i B. Oznacza to, że średnie oceny populacji są sobie równe, µA = µB.
Czy próbka jest wystarczająco liczba dla analizy porównawczej two-sample t?
Zwiększenie rozmiaru liczebności próbek prowadzi do zwiększa mocy testu. Zbyt małe próbki podważają wiarygodność testu. Zbieranie zbyt liczebnych zbiorów jest niepotrzebną stratą zasobów
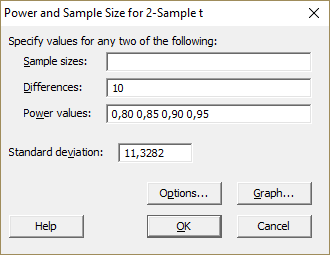
Określając moc testu (w naszym przypadku 95
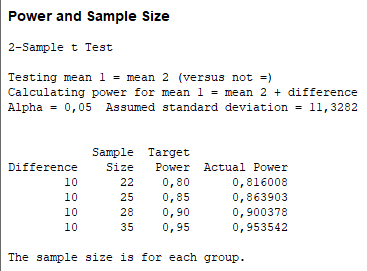
Z poprzednich obliczeń uzyskano informację, że wspólne odchylenie standardowe jest równe 11,3282.
Przeprowadzony został test liczebności pomiarów dla współczynników ufności 80
Test wykazał, że dla spółczynnika ufności na poziomie 95
Liczebność obserwacji użytych w analizie procedur A i B wynosiła 40, więc badanie jest wiarygodne.
Możliwe jest również obliczenie mocy testu dla określonej liczebność próby.
