W poprzednim wpisie, używając statystyki opisowej analizowaliśmy średnie, odchylenia oraz skrajne wartości w zależności od dnia tygodnia, w którym dokonano pomiarów.
Dzisiaj użyjemy jednoczynnikowej analizy wariancji ANOVA, jednej z najczęściej stosowanych narzędzi porównywania dwóch populacji.
ANOVA jest metodą statystyczną testującą istotność różnic pomiędzy średnimi w kilku populacjach.
Jednym z najważniejszych warunków stosowania ANOVA jest ujednolicenie danych. Z wcześniejszych analiz wiemy, że statystyki czasu załadunku w różnych magazynach, różni się od siebie. Dlatego do porównania załadunków wg. dni tygodnia wybierzemy tylko jeden magazyn: Poznań.
Z danych wyrzucamy pomiary z soboty i niedzieli. Te dni są dla magazynu nietypowe.
Minitab przyjmuje domyślny współczynnik ufności: 0,95
W efekcie uzyskujemy następujące wyniki analizy:
Jednoczynnikowa analiza wariancji ANOVA polega na testowaniu równości średnich kilku populacji mających jeden czynnik wspólny (tzw. czynnik klasyfikujący). W tym przypadku czynnikiem klasyfikującym jest czas załadunku. Wyniki pomiarów z każdego dnia tygodnia tworzą oddzielne populacje, które teraz testujemy.
W większości testów statystycznych posługujemy się hipotezami statystycznymi:
Hipoteza zerowa: wariancje analizowanych populacji są sobie równe
Hipoteza alternatywna: wariancje analizowanych populacji nie są sobie równe
Minitab przyjmuje domyślny współczynnik ufności: 0,95
Minitab w swojej statystyce stosuje odchylenie standardowe, które jest kwadratem wariancji.
Jeśli wartość p jest mniejsza lub równa wstępnie ustalonemu poziomowi
istotności (poziomowi α), wówczas hipoteza zerowa jest odrzucana, a za
prawidłową uznawana jest hipoteza alternatywna.
Jeśli wartość p jest większa niż poziom istotności (α), nie można odrzucić hipotezy zerowej i uznać hipotezy alternatywnej za prawdziwą.
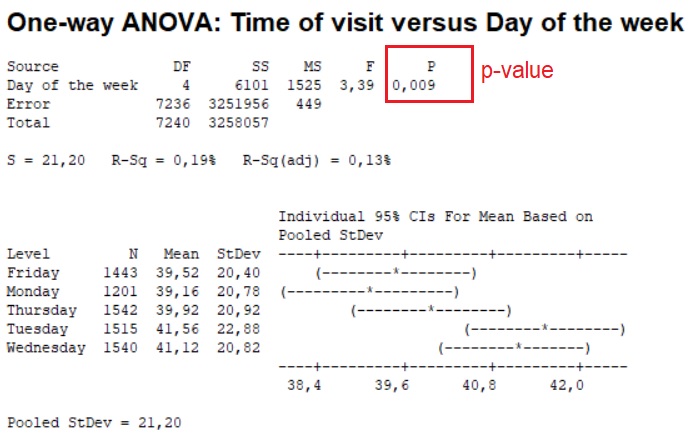
P-value w naszym przykładzie wyniosło 0,009.
Jeżeli p-value (czyli poziom prawdopodobieństwa wspólny w porównaniach populacji) jest mniejsze od przyjętego współczynnika ufności α =0,05, wtedy odrzucamy hipotezę zerową. Wtedy uznajemy, że wariancje porównywanych populacji istotnie różnią się od siebie.
W naszym przypadku są podstawy do odrzucenia hipotezy zerowej, ponieważ p-value wyniosło 0,009 i było mniejsze od współczynnika ufności α =0,05.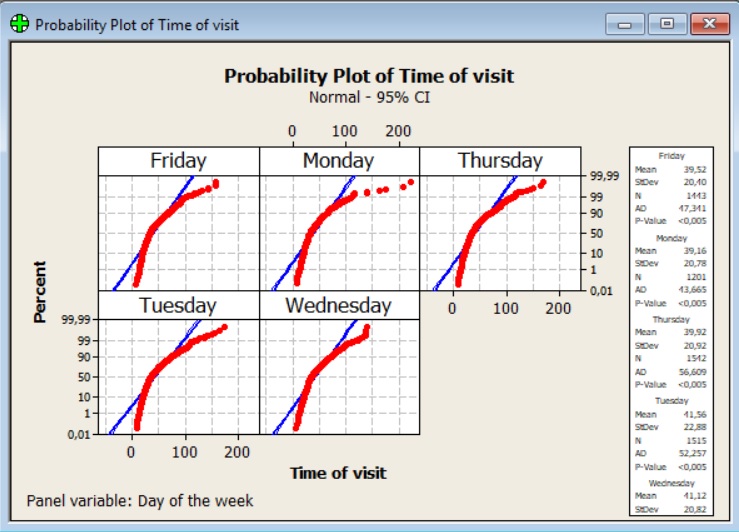
Aby porównać populacje należy wybrać określony asortyment.
Aby przeprowadzić test ANOVA muszą być zachowane dwa warunki:
-
Próby zostały pobrane niezależnie od siebie w każdej z populacji
-
Każda populacja ma rozkład normalny o tym samym odchyleniu standardowym (kwadracie wariancji).
Test AD nie potwierdził, że porównywane populacje mają rozkłady normalne i te same odchylenie standardowe.