Inżynier nadzorujący proces produkcyjny ma za zadanie monitorować jaka jest zmienność wymiarów produkowanego elementu skrzyni biegów. Nie może on sobie pozwolić na badanie każdej sztuki. Dlatego też dokonuje on pomiaru co 20 sztuki produkowanego detalu.
Zmierzył dotąd 30 detali i uzyskał wariancje z próby 23 716 (odchylenie standardowe z próby 154 µm = 0,154 mm). Mamy n-1 stopni swobody, czyli w tym przypadku 20-1=29. Przedział ufności 95%.
Kalkulator do przeliczenia jednostek: http://aztekium.pl/units.py
Wzór na obliczenie przedziałów za pomocą rozkładu chi-kwadrat (18.1).
Po podstawieniu do wzoru 18.2 inżynier dowiedział się, że z prawdopodobieństwem 95% wariancja σ2 badanej populacji wynosi od 15 050 do 42 985. Oznacza to, że odchylenie standardowe populacji znajduje się od 123 µm do 207 µm.
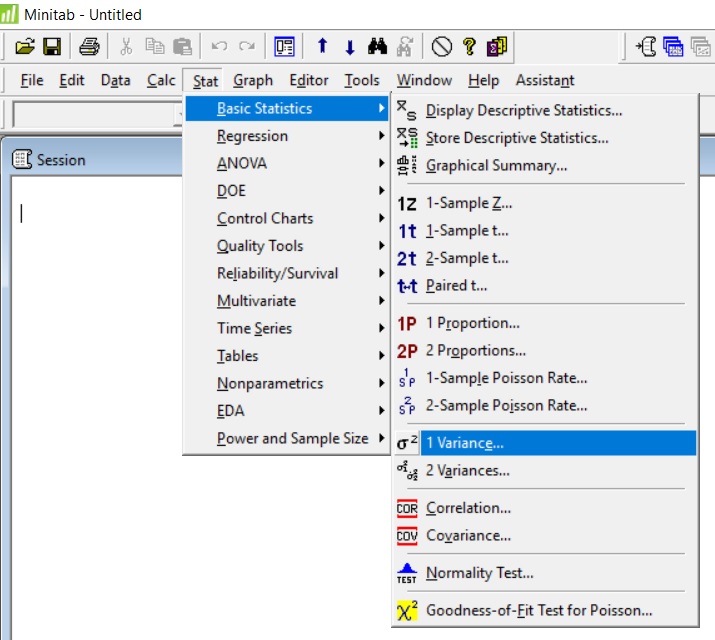
Jak obliczyć przedziały dla wariancji populacji σ2 za pomocą rozkładu chi-kwadrat