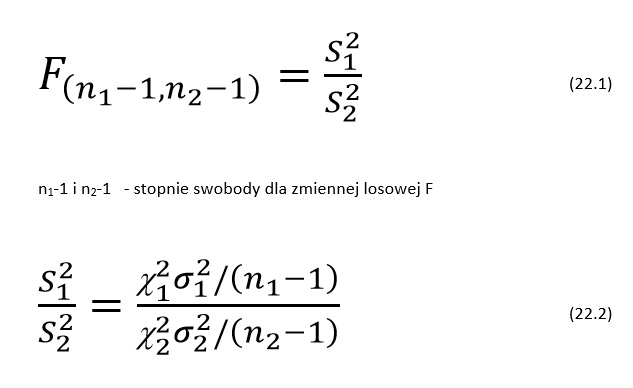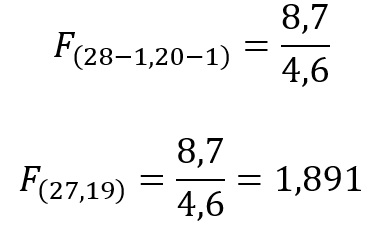Rozkład f został wymyślony m. in. po to, aby porównywać wariancje dwóch populacji o różnych stopniach swobody.
Przypomnijmy, że rozkład Chi-kwadrat porównywał wariancję z populacji posiadających tą samą liczbę stopni swobody. Rozkład f potrzebuje dwóch stopni swobody: k1 – stopnie swobody licznika (numerator df) oraz k2- stopnie swobody mianownika (denominator df).
Gdy są dwie próby, są też dwie zmienne losowe wariancje S12 oraz S2 o określonej liczbie stopni swobody n1-1 oraz n2-1.
Wzór na sprawdzenie równości wariancji w dwóch populacjach o rozkładzie normalnym.
Jak porównywać wariancje dwóch populacji o różnych stopniach swobody?
Telefoniczne centrum obsługi klienta wprowadziło dla pracowników szkolenia z zakresu komunikacji. Jednym z celów było zmniejszenie odchylenia standardowego (czyli kwadratu wariancji) czasu trwania rozmów.
Zebrano dwie małe próby przed i po szkoleniu.
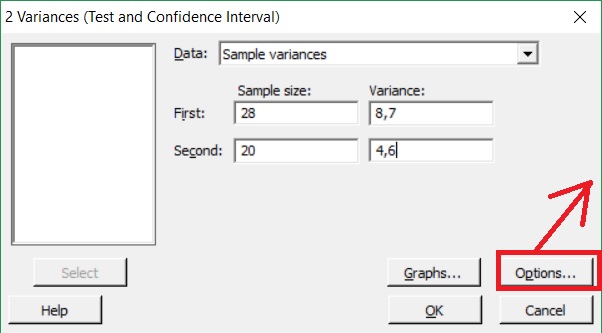
28 pomiarów przed szkoleniem wykazało wariancje na poziomie S12 = 8,7
20 pomiarów po szkoleniu wykazało wariancję na poziomie S22 = 4,6
Wariancje S1 i S2 są estymacją wariancji całej populacji µ1 i µ2.
Stawiamy hipotezę do testu f:
H0: obie wariancje populacji są jednakowe µ1 = µ2
H1: obie wariancje populacji nie są jednakowe µ1 ≠ µ2
Aby porównywać wariancje dwóch populacji o różnych stopniach swobody stosujemy wzór 22.1.
Dla współczynnika ufności 95
Oznacza to że jest zgodnie z hipotezą zerową H0 nie ma podstaw do uznania, że wariancje populacji są od siebie różne. Szkolenia pracowników nie zmniejszyły wariancji.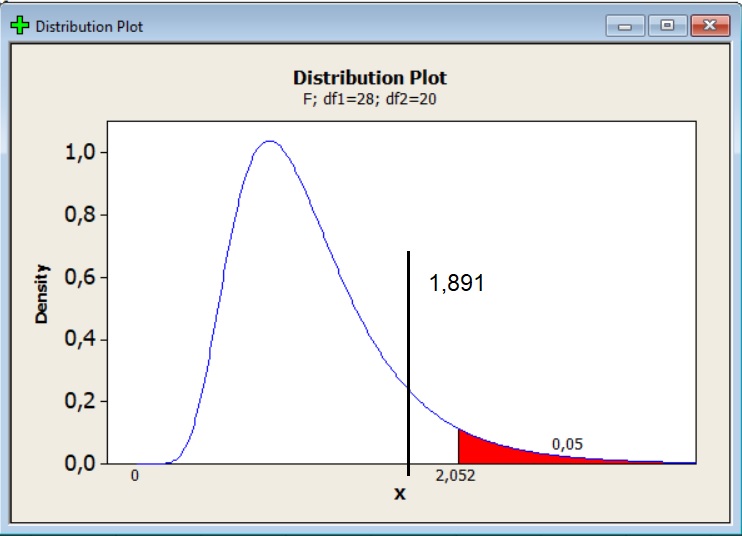
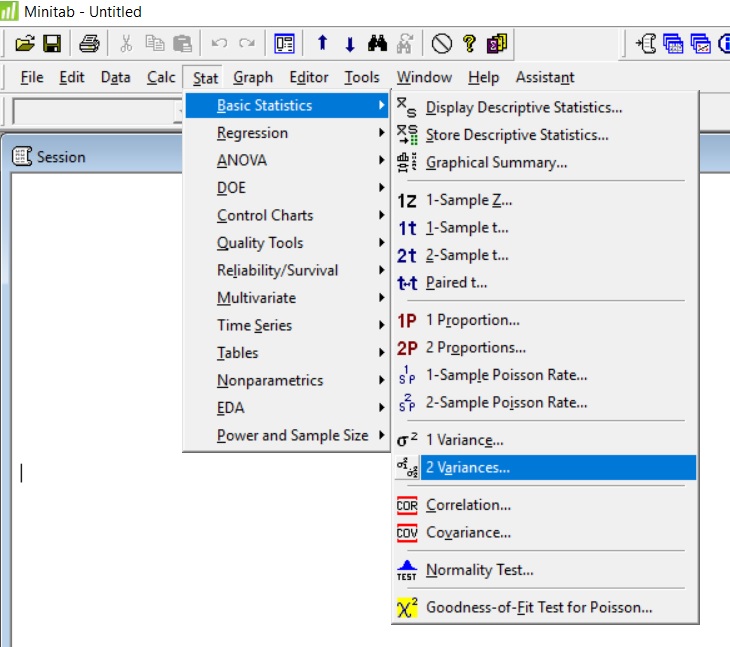
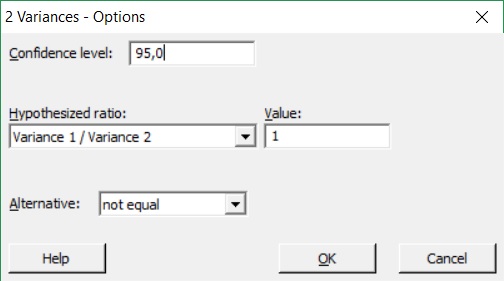
Jak porównywać wariancje dwóch populacji o różnych stopniach swobody za pomocą programu Minitab?
P-value jest większe od 0,05, czyli jest większe od obszaru odrzucenia.
Rozkład f jest skutecznym narzędziem, aby porównywać wariancje dwóch populacji o różnych stopniach swobody.