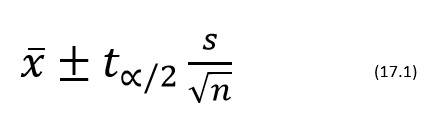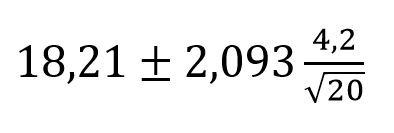W poprzednim wpisie poznaliśmy rozkład t.
Należy zapamiętać, że do szacowania (estymacji) wartości losowych populacji czy średnich stosuje się rozkład t tylko wtedy, gdy:
Rozkład prawdopodobieństwa populacji jest zbliżony do rozkładu normalnego
Gdy nie jest znane odchylenie standardowe populacji σ
Rozkład T jest podobny do rozkładu normalnego, przy bardzo dużej lub nieskończonej liczbie stopni swobody rozkład t jest identyczny ze standaryzowanym rozkładem normalnym Z.
Użycie rozkładu t do szacowania średniej z populacji
Pewien inżynier chciał dowiedzieć się jaki jest średni poziom w zbiorniku płynu chłodzącego.
Dokonał on 15 pomiarów poziomu płynu, n=20. Średnia poziomu wynosiła 18,21 cm przy odchyleniu standardowym s= 4,2 cm. Inżynier przyjął 95% przedział ufności.
Dla wyznaczenia przedział w jaki przy 95% prawdopodobieństwem znajdzie się średni poziom cieczy chłodzącej stosuje się wzór:
gdzie:
średnia µ i odchylenie standardowe populacji σ nie są znane.
Wartość dla 95% przedziału ufności obliczamy ze wzoru 16.2.
Z tabel prawdopodobieństwa w rozkładzie t odnajdujemy wartość 2,093 dla α/2=0,025 i n-1 stopni swobody (20-1=19). Teraz podstawiamy do wzoru 17.1.
Inżynier obliczył za pomocą rozkładu t, że prawdopodobieństwem 95% średni poziom płynu chłodzącego waha się między 16,2443 a 20,1756 cm. Aby uzyskać bardziej precyzyjną informacje inżynier powinien zwiększyć liczbę stopni swobody df. Innymi słowy mówiąc inżynier powinien zwiększyć ilość pomiarów.
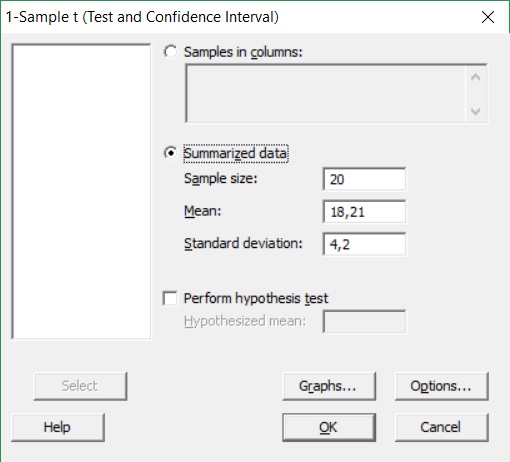
Użycie rozkładu t do szacowania średniej z populacji za pomocą programu Minitab