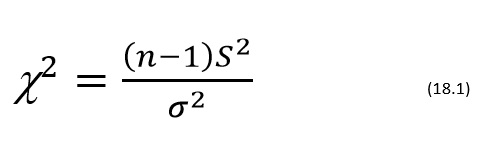Dziś poznamy trzeci bardzo ważny rozkład prawdopodobieństwa: rozkład chi-kwadrat
Przedmiotem pracy nad jakością jest przede wszystkim zmienność utożsamiana ze słabością, błędami i niedoskonałościami procesu. Six Sigma przede wszystkim dąży do minimalizacji zmienności. Aby robić to skutecznie należy, najpierw mieć informacje o zmienności. Do tej pory zajmowaliśmy się estymowaniem wartości średniej populacji na podstawie próbek. Przy małej próbce mogliśmy to robić za pomocą rozkładu t, przy dużej próbce za pomocą rozkładu Z (rozkładu normalnego).
Dzisiaj dochodzimy do najbardziej praktycznego zastosowania testów. W praktyce Six Sigma dużo ważniejsze jest estymowanie zmienności niż estymowanie średniej populacji. Wystarczy przypomnieć sobie jakie jest główne zadanie kart kontrolnych Six Sigma.
Zmienność populacji jest reprezentowana przez odchylenie standardowe populacji σ lub przez wariancję populacji σ2
W praktyce jest bardzo trudno lub nie jest możliwe zbadanie całej populacji, dlatego metodyka statystyczna wyspecjalizowała się w estymacji odchylenia standardowego σ na podstawie odchylenia standardowego próby S oraz średniej z próby X. Pamiętajmy, że estymacja jest przedstawiana jako przedział w jakim znajduje się estymowana wartość, przy określonym współczynniku ufności.
Rozkład chi-kwadrat – założenia teoretyczne
Do wyznaczania przedziałów ufności dla estymowanej wariancji populacji σ2 (czyli kwadratu odchylenia standardowego populacji σ) powstał specjalny rozkład chi-kwadrat (2).
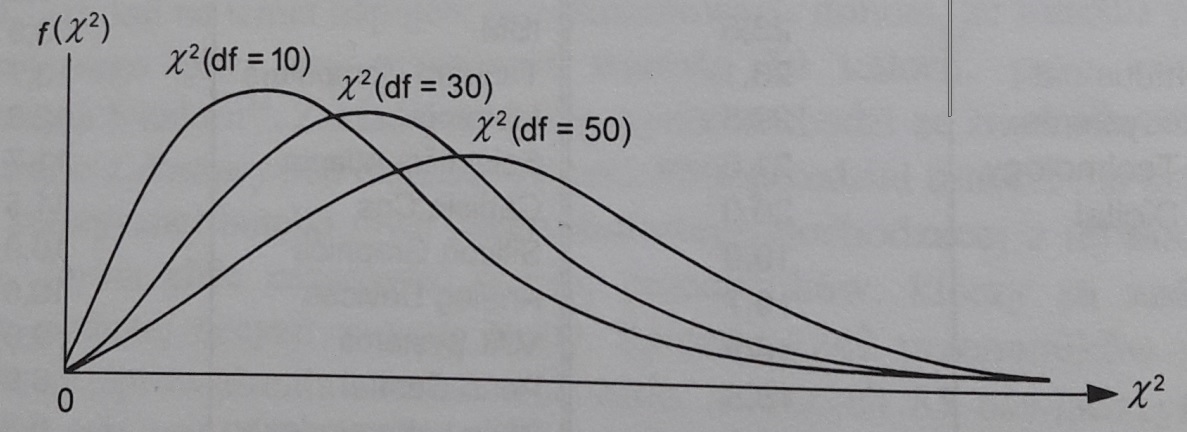
Rozkład chi-kwadrat jest wyliczony na podstawie rozkładu normalnego. Jest to rozkład prawdopodobieństwa sumy kwadratów zmiennych losowych w rozkładzie normalnym.
Ponieważ suma kwadratów nie może przyjmować wartości ujemnych, rozkład nie jest symetryczny, jest prawostronnie skośny. Podobnie jak w rozkładzie t, o kształcie rozkładu chi-kwadrat decyduje liczba stopni swobody df. Czym więcej jest stopni swobody, tym bardziej rozkład chi-kwadrat upodabnia się do rozkładu normalnego.
Rozkład chi-kwadrat ma dwie ważne właściwości:
- średnia rozkładu jest równa liczbie stopni swobody df,
- wariancja rozkładu jest równa liczbie stopni swobody df razy dwa.
Rozkład chi-kwadrat powstał po to, aby estymować wariancje populacji σ2 na podstawie próby.
Estymacji przez rozkład chi-kwadrat dokonuje się na podstawie poniższego wzoru:
Powyższe równanie jest prawdziwe, jeżeli próba została pobrana z populacji o rozkładzie normalnym.
Na podstawie wzoru 18.1 wyznaczamy wzór na przedział ufności do estymacji wariancji populacji σ2.
Oba końce przedziałów mają inne wzory, ponieważ rozkład chi-kwadrat nie jest symetryczny.
W następnym wpisie pokażę, jak szacować wariancje populacji za pomocą rozkładu chi-kwadrat w programie Minitab.